Muestras de información a medias

Revisado 24 septiembre 2023

Resumen

Al manejar información [numérica] sobres temas reales, no triviales, es muy habitual que se usen valores medios, y es igualmente habitual que el que maneja esa información no sea consciente ni de qué muestras se han usado para esas medias (cuál es la población total) ni de que sean valores medios y lo que implica, aunque a veces se manejan  deliberadamente ciertas muestras y valores medios para manipular la información facilitada y para asumir la información que uno quiere creerse.
Es un tema que ha salido en varios posts, e intento centralizar ideas aquí: creo que es algo esencial tener unos conceptos básicos asociados a medias para saber interpretar y presentar datos. Enlaza con anumerismo, mala información, desinformación y manipulación estadística.
Todo depende del contexto y nunca es bueno generalizar y decir que la media no sirve para nada; hay un ejemplo real donde el valor medio es casi lo más importante de todos los datos, que es la temperatura media del planeta asociada al calentamiento global.
A veces se cita que además de medidas hay que añadir desviación, y también correlación entre variables, pero también hay que visualizar eso no siempre es suficiente. Muestro una imagen de un artículo que recomiendo leer, y muestra la importancia de la interpretación de datos, y de su representación y visualización además de dar simplemente números.



The Datasaurus Dozen. Same Stats, Different Graphs: Generating Datasets with Varied Appearance and Identical Statistics through Simulated Annealing
https://www.autodeskresearch.com/publications/samestats

En ese artículo se cita
...make both calculations and graphs.
Both sorts of output should be studied;
each will contribute to understanding.
F. J. Anscombe, 1973
(and echoed in nearly all talks about data visualization...)
y se incluye esta imagen



Algunos posts relacionados (los cito dentro del post)


Detalle

Índice
  • Introducción; el título del post
  • La media es una información débil e incompleta
    • Medias en las que participa uno mismo o personas conocidas
    • Visualización de datos y no solo cifras de datos agregados resumidos
    • Cifras significativas
    • Media, mediana, moda, varianza
    • El error de aplicar media a una muestra de tamaño pequeño
    • Desprestigiar la información media con cherry picking
  • La media se usa incorrectamente
    • Ratios
    • Riqueza
    • Salario
    • Cambio climático: cuando la media sí importa 
    • Gasto medio de alumno
    • Segregación alumnos
    • Calificaciones medias
    • Gasto por persona e impuestos 
    • Clase media
    • Tiempos medios 
    • Algunas ideas pendientes 

Introducción; el título del post

El título del post es deliberadamente polisémico, y enlaza con la frase "no hay peores mentiras que las verdades a medias", pero es algo más específico y un juego de palabras: no se trata solamente de la falacia de la verdad a medias o de decir media verdad, sino de usar medias en la información. Usar medias estadísticas en la información es dar información a medias.
https://es.wikipedia.org/wiki/Falacia_de_la_verdad_a_medias
https://es.wikipedia.org/wiki/Media_verdad
A nivel técnico y físico me recuerda el uso de los términos de vida media y media vida en radiactividad, conceptos distintos pero ambos con valor de tiempo, que considero son una mala traducción de mean (promedio, estadística) y half (parte, incompleto) porque en español la palabra media es polisémica.
Intento jugar con ambos significados de media, mostrando como dar promedios estadísticos da información incompleta.
El uso que se hace de datos de media a veces "no tiene ni media hostia"
https://www.fundeu.es/noticia/elogio-de-la-hostia-5762/
y en general es "ir a medias" porque supone "Colaborar o participar a medias en algún asunto.", y "a medias" tiene el significado "Algo, pero no del todo, incompletamente."
https://dle.rae.es/?id=OlQ6yC8
También la palabra del título muestra tiene cierta polisemia: https://dle.rae.es/?id=Q0cz7HH como una porción de algo, y como ejemplo o modelo de algo.

La media es una información débil e incompleta

A menudo hay que dar información de ciertos asuntos que tienen gran cantidad de datos, y tristemente hay que dar algo muy breve y resumido para "resúmenes ejecutivos" o "prensa rápida" que permita leerlo rápido.
>Esto da para hablar de presentaciones ejecutivas y uso de powerpoint, que es para otro post.

La media resume en un único valor muchos otros valores, pero lógicamente en el proceso se pierde  información. Es una medida de centralización.
Vale, sí, dar la media es más información que no dar nada, pero aunque decirlo parezca obvio, NO, LA MEDIA ES UN RESUMEN Y NO INFORMA DE TODO LO QUE ESTÁ RESUMIENDO.

Hay frases tópicas, con mínimas variaciones, que resumen esto.
Hay una frase tan tópica que está, ejem, en la web del INE
https://www.ine.es/explica/docs/pasos_conceptos_parte2.pdf#page=23
"Si una persona se come cuatro pollos y otra ninguno, en media se han comido dos cada una."


En la página 33 del mismo documento
¿Qué conclusión sacamos entonces? Que las medidas de centralización son muy cómodas y útiles, pero deben venir siempre acompañadas de una medida de dispersión, que nos indica si realmente la medida de centralización resume bien la muestra (cuando la medida de dispersión es pequeña) o si por el contrario no recoge bien toda la información (medida de dispersión alta).

En página 43
Y recuerda: una temperatura media anual de 15ºC puede significar dos cosas: que o bien en esas ciudad todos los días hay 15ºC, o bien que en esa ciudad a veces hay 0ºC y a veces 30ºC. 

La media de unos datos debe ir acompañada de la dispersión de esos datos o da información completa; da información a medias

 Para mi un ejemplo perfecto es el que ponía mi profesor de la materia de "Investigación operativa y teletráfico" en la universidad, que tengo perfectamente grabado:

"Os planteo esto:
En la parada del autobús de al lado pasa, de media, un autobús cada hora.
Si yo llego a la parada ¿cuánto creéis que voy a esperar, de media, hasta que llegue un autobús?"

 Respuesta inmediata habitual: de media, se espera media hora.

 "Pues no, porque no he indicado en qué intervalo he realizado la media ni su varianza. 
Imaginaos que pasasen 24 autobuses al tiempo, una vez al día: la media seguiría siendo 1 autobús cada hora, pero mi tiempo de espera medio sería de 12 horas"

Otro ejemplo creo que típico es que es fácil ver que el número medio de piernas que tiene la población siempre es menor que 2, ya que alguna persona coja habrá, pero eso no refleja la realidad, porque el número de piernas solamente tiene valores enteros.

Otros ejemplos que he puesto en Twitter (asociados a ratios, que trato luego)

https://twitter.com/FiQuiPedia/status/878587707383062529
media sin dispersión no da info real: si 9 personas cobran 0€ y otra 10€, la media es 1. Ratio legal primaria es 25 por grupo, no 25 media

otro ejemplo: 9 personas viven 100 años y una fallece con 0; vida media son 90 años. En educación CRA suelen tener ratios bajos y baja media

Ante esos ejemplos alguien dice "esos ejemplos son extremos, porque en la distribución de datos no hay valores tan distintos". Son ejemplos extremos para mostrar lo erróneo de mirar solamente la media, y LA MEDIA SIN MÁS NO DA NINGUNA INFORMACIÓN DE DISPERSIÓN para saber si estoy o no en un caso extremo. Las personas que argumentan que son casos extremos ni se molestan en mirar información de dispersión para ver si lo que dicen en cierto (un ejemplo asociado con valores extremos es la renta, se trata luego)

Pero hay todavía más: ni la media ni la dispersión informan explícitamente del tamaño de la muestra, ni de cómo se ha realizado. A veces al dar datos de media se asume que es sobre un global de la población (se considera CENSAL, por ejemplo, salario medio es la media de todos y cada uno de los  salarios), pero se puede concretar mucho. A veces los datos son ESTIMADOS con una MUESTRA, que son solamente ciertos casos, supuestamente elegidos al azar, que se considera que permiten estimar lo que ocurre en el global de la población. A veces se realizan solamente acotados a ciertas casos (una zona geográfica (España, una comunidad), un sector (público, privado), un ámbito profesional (médicos, docentes), un sexo), y cuando no se hacen acotados, la muestra tiene solamente ciertos datos de cada uno de los casos y esas submuestras no permiten estimar lo que ocurre en todos.

Algunos ejemplos estimados con muestras:
  • Audiencias de programas: se da un % de audiencia, y se dan valores de número de personas en toda España que estaban viendo o escuchando un programa de TV o radio algo, cuando solamente se está midiendo a un grupo de personas.
  • Desempleados, Abandono escolar temprano: se estiman con EPA (Encuesta Población Activa) que solamente hacen ciertas personas, y con esa muestra se da un valor para toda España.
El ejemplo de imagen inicial del post es citado aquí
https://francis.naukas.com/2019/03/28/metameros-cuidado-con-las-medias-las-desviaciones-tipicas-y-las-correlaciones-estadisticas/

Medias en las que participa uno mismo o personas conocidas

Hay un tema que enlaza con sesgos: qué pasa cuando uno mismo es miembro de la muestra.
Si resulta que escuchamos frases del estilo

"Cada español
...gasta 60 € en la lotería de navidad
...consume 50 litros de cerveza al año
..."
Y resulta que yo no juego nada / no bebo nada, ese dato me toca especialmente.
Pienso que hay algo mal, o que "alguien está jugando mucho más de 600 € / bebiendo mucho más". Es parcialmente correcto, pero no del todo, porque esas opiniones suelen hablar de moda, no de medias: mi caso baja la media, y tiene que haber gente que la suba para que de ese valor, pero no se puede asumir una dispersión concreta en el resto de la población, que influye en el tamaño de la muestra.
Enlaza con el ejemplo del pollo: si la población es 2, y yo no como pollo, sí sabemos lo que pasan en el resto. Pero si la población es 1 millón, y yo no como ninguno pero la media es 2, puede que haya muchos que no coman nada y algunos que coman miles.
Esto se ve mejor con otro ejemplo: escuchamos que el salario medio son 22000 € y resulta que yo cobro 20000 €. Puedo pensar que si mi valor es menor, en general se cobra más / que cobro menos que la mayoría, pero no totalmente cierto si la moda son 16000€.

También enlaza con Ratios en educación: estadísticas y realidad; cuando salen datos de ratios y la media es menor que la realidad de sus grupos, muchos comparan y a veces dudan de los datos porque se alejan de los valores de sus grupos.

También enlaza con la segregación: "los privados con concierto no segregan, porque en mi centro tenemos muchos inmigrantes / ACNEEs"

He repetido mucho la afirmación: "lo puntual, sin negar que sea cierto, no niega lo global"


Visualización de de datos y no solo cifras de datos agregados resumidos

En el resumen del post comienzo intentando explicar esta idea, enlazando imágenes y texto que no repito aquí.

Actualmente hay cada vez mejores opciones de visualización de datos, pero se hay quien se empeña en verlos de manera agregada en la que se pierde información.
La manera de presentar datos es muy importante.
Y a veces interviene de nuevo el sesgo de lo que uno quiere interpretar de los mismos datos y pretende convencer a los demás que dicen esos datos.
Sin manipular los datos, está el truco sencillo y rápido de truncar los ejes de las gráficas para hacer más o menos relevante cierta variación. También está el truco de comparar los datos o agregarlos como haga falta (cierto intervalo temporal, comparar datos medios con no medios), para conseguir que digan lo que se quiere decir.

Pongo un ejemplo inventando para ilustrar lo que quiero decir (donde pone paro, cámbiese por abandono escolar temprano o lo que uno quiera. Se pueden buscar malos usos en prensa y comunicados

-En este trimestre el paro sube x personas
-En este trimestre el paro sube un y%
-De este trimestre al del año anterior el paro baja un z%
-El valor del paro en este trimestre es el menor en enero en los últimos a años
-La subida del paro en este trimestre es la más baja en %  / en cantidad de los últimos a años
-El paro sube en este trimestre en la región b la menor cantidad comparada con las regiones c, d y e
..." 

Una buena presentación de datos los muestra visualizados, y permite a cada persona que los ve analizarlos y sacar sus conclusiones.
Si los datos están "resumidos", y ya presentan una conclusión, es complicado realizar otro análisis que sí permitiría tener esos datos.

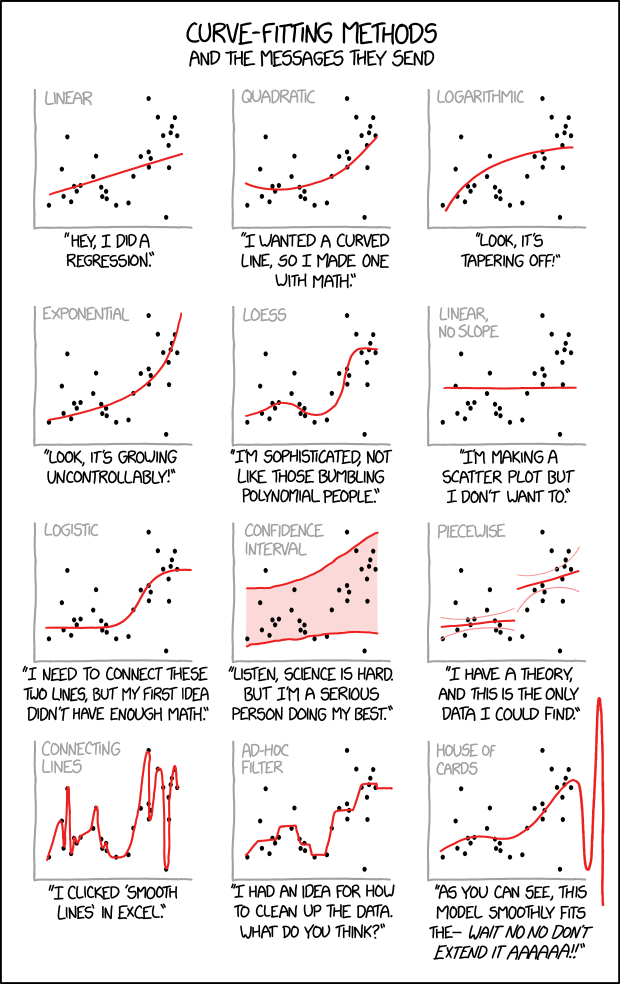
Building calibration curves
https://kimikarte.blogspot.com/2016/11/building-calibration-curves.html
Que cita "Curve-fitting methods, and the messages they send"
https://xkcd.com/2048/



También se puede citar este hilo donde se muestra la imagen inicial animada
Se habla más de usar cuartiles (o quintiles, o deciles ...) como medida de caracterizar.

https://twitter.com/Picanumeros/status/859752474865016832
Con respecto de este GIF, que está siendo utilizado para defender a ultranza las visualizaciones de datos: https://i2.wp.com/blog.revolutionanalytics.com/downloads/DataSaurus%20Dozen.gif

Me parece que se está sobredimensionando el tema. Miles de retweets enterrando la estadística descriptiva por algo que tiene explicación.
Lo que diferencia a esas nubes es su MORFOLOGÍA, no su CENTRALIDAD ni su DISPERSIÓN ni su DEPENDENCIA (= lo que miden esos 3 estadísticos).
Las medias son iguales: una media es el centro de gravedad de todos los puntos. Nos dice "por donde quedan".
Todas las nubes de puntos se sitúan en el mismo rango de datos, y están centradas en torno al mismo punto. Es lógico que tengan igual media.
Las desv. típicas son iguales: de nuevo, hay que fijarse en las similitudes que tienen esos conjuntos de datos pese a su distinta morfología
El rango es el mismo, el centro de gravedad también. Y los puntos en todas esas formas están + ó - uniformemente dispersos dentro del rango
Quiero decir, no se ven burradas como por ejemplo dos nubes de puntos perfectamente diferenciadas dentro de una. Les une la uniformidad.
La correlación es algo más particular. Se puede explicar el por qué da siempre lo mismo (la forma de las nubes nunca es lineal, p. ej.)
Pero en todo caso, una correlación entre 2 variables NO caracteriza un conjunto de datos. Que tengan la misma correlación no significa nada.
Antes de apoyar ciegamente usar el "dataviz" por encima de todo, ¿por qué no considerar las opciones que nos brinda la estad. descriptiva?
Posiblemente revisando los cuartiles (las auténticas medidas de FORMA) ya podríamos ver los cambios entre conjuntos.
Y no pretendo con esto demonizar las visualizaciones de datos. Las uso con asiduidad. Pero no les demos más importancia de la que tienen.
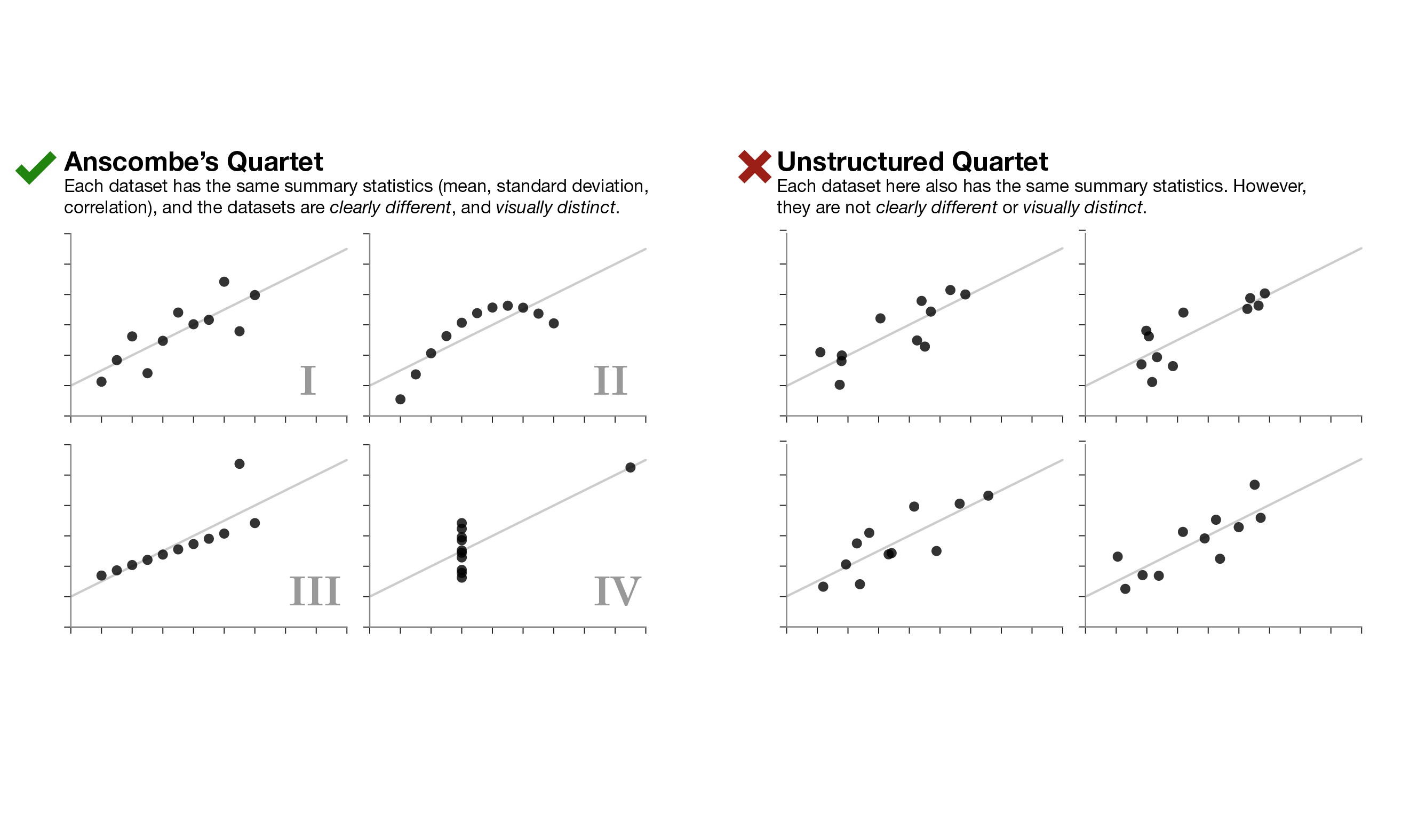
PD: comparar este GIF con el cuarteto de Anscombe me parece comparar churras con merinas. Anscombe muestra efectos de outliers (este no).

7 septiembre 2023

What This Graph of a Dinosaur Can Teach Us about Doing Better Science

“Anscombe’s quartet” and the “datasaurus dozen” demonstrate the importance of visualizing data

https://www.scientificamerican.com/article/what-this-graph-of-a-dinosaur-can-teach-us-about-doing-better-science/


Cifras significativas

Las cifras significativas es algo importante pero también poco conocido. Cuando se hacen medias se obtienen muchos decimales, se pueden querer mostrar datos agregados con muchas cifras, pero no tiene sentido.
A veces mostrar muchos decimales enlaza con la trampa de truncar ejes y amplificar la variación de valores, cuando los valores con muchas cifras pueden no tener sentido.

Ejemplos (los separo de los ejemplos posteriores más centrados en uso incorrecto de medias)

En los resultados PISA se habla a menudo de "variación de x puntos", siendo ese valor de una cifra o poco más, cuando el valor total ronda los 500.

6 diciembre 2016
nforme PISA: España sigue a la cola en Matemáticas y Ciencias aunque mejora en Lectura
https://www.elespanol.com/sociedad/20161206/176232388_0.html

En España se examinaron 37.205 alumnos de, por primera vez, todas las comunidades autónomas.  
...
En Lectura, los estudiantes españoles de 15 años logran una puntuación media de 496 puntos, ligeramente superior a la de la OCDE (493) y a la de la Unión Europea (494).

1/494 =0,2%. Sí se indica el tamaño de la muestra, aunque comparar esos valores parece absurdo. Si esa es la muestra para todas las CCAA, la muestra para cada comunidad será menor, y el margen de error mayor.

5 diciembre 2017
España se queda 12 puntos por debajo de la media de la OCDE en comprensión lectora
https://www.abc.es/sociedad/abci-espana-queda-12-puntos-debajo-media-ocde-comprension-lectora-201712051043_noticia.html

La puntuación total del estudio internacional de progreso en comprensión lectora, realizado por la Asociación Internacional para la Evaluación del Rendimiento Educativo (IEA), ha sido de 513 puntos, doce menos que la media de la OCDE y once que la Unión Europea.
...
los países de nuestro entorno han obtenido menor puntuación que en la edición anterior: Portugal (-13 puntos), Francia (-9 puntos) y Alemania (-4 puntos). 


12/513 es del orden del 2%, 4/513 es menor de un 1% y habría que saber la muestra y el margen de error.


15 junio 2019
https://twitter.com/mrebollo/status/1139820195508305921
Necesario leer juntos y No te fies de los datos ni de esos gráficos

Error muy común. Tenemos tres valores 7, 7 y 5 Queremos calcular la media. Sumamos y dividimos entre 3. El resultado? 6,333333333333333333333 ¿Con cuántos decimales.. mejor... con cuántas cifras significativas debe expresarse esa media?
Qué distancia a la media consideraremos que es mucha o poca? De nuevo muy dependiente de la dispersión de los datos. Dar una media con muchos decimales y sin mencionar la dispersión es cuando menos confuso y, en muchos casos, malintencionado

https://lacienciaparatodos.wordpress.com/2014/06/10/de-una-estadistica-mal-hecha-puede-deducirse-nada/ 
Otra cita creo que procedente para ver lo absurdo de intentar usar más cifras de las que tienen sentido según los datos.

http://elprofedefisica.naukas.com/2016/02/15/otra-prueba-de-las-bases-fisicas-de-la-homeopatia-o-no/

Por supuesto, si la sensibilidad del instrumento (lo mínimo que puede apreciar) es una cantidad mayor, ésta es la que te va a limitar la precisión. Es decir, no me importa que midan varias veces, hagan los números y obtengan un valor de 0,00003 ± 0,00016, porque si lo mínimo que puede apreciar tu instrumento es 0,001 el verdadero valor es 0,00003 ± 0,001; y eso en mi pueblo se redondea como 0,000 ± 0,001. Harto estoy de explicárselo a mis alumnos cada año, para que ahora ventan unos aprendices de científico a tomarme el pelo.


Media, mediana, moda, varianza

He hablado de media pero no la he definido explícitamente, asumiendo que se conoce. También he citado varianza. No voy a reinventar la rueda explicándolo: los enuncio en una frase y cito referencias
  • La media: resultado de sumar todos los datos de la muestra y dividir entre el total.
  • La moda: el valor que más se repite en los datos de la muestra.
  • La mediana: el valor que queda en la posición central al ordenar los datos de la muestra.
  • Varianza: una medida de cómo de separados están los datos respecto de la media.

https://www.ine.es/explica/docs/pasos_conceptos_parte2.pdf

Alguien dirá ¿para qué narices explicas eso, si lo sabe todo el mundo que tiene la educación básica?
Pues sí, aparece que el currículo, Real Decreto 1105/2014, de 26 de diciembre, por el que se establece el currículo básico de la Educación Secundaria Obligatoria y del Bachillerato.

Matemáticas. 1º y 2º ESO
Bloque 5. Estadística y probabilidad
Matemáticas orientadas a las enseñanzas académicas. 3º ESO
Bloque 5. Estadística y probabilidad
Matemáticas orientadas a las enseñanzas aplicadas. 3º ESO
Bloque 5. Estadística y probabilidad

Pero eso no quiere decir que se conozcan y se manejen bien
Aquí se puede ver un ejemplo en un programa de TV y por un economista
https://twitter.com/FiQuiPedia/status/1079307513651179520
Épica Batalla de Pizarras: Juan Ramón Rallo y Daniel Lacalle VS Gonzalo Bernardos y Eduardo Garzón
Minuto 32
https://www.youtube.com/watch?v=6R5eoz91P3o
Vídeo original
https://www.lasexta.com/programas/sexta-noche/la-pizarra/daniel-lacalle-los-paises-que-han-mejorado-su-empleo-y-su-renta-son-los-que-han-flexibilizado-la-contratacion_20170212589fba2b0cf2f719cbefb232.html 

Para explicar algo lo mejor son los ejemplos donde se pueda visualizar el conjunto total de datos, distintas medias, moda, varianza ... y cómo se usan incorrectamente

 

https://twitter.com/Picanumeros/status/1372099384180150272

Si un conjunto de datos es...
🔼Simétrico 👉 Media = mediana = moda
📉 Asimétrico por la derecha 👉 Moda < Mediana < Media
📈 Asimétrico por la izquierda 👉 Media < Mediana < Moda

Estas reglas NO SIEMPRE se cumplen, pero sí de manera habitual. Como en la distribución Beta 👇

 



El error de aplicar media a una muestra de tamaño pequeño

Es un error de concepto asociado a anumerismo: si me indican que el valor medio es de cierto % en una muestra grande, a veces se afirma errónamente que en una muestra pequeña se cumple esa misma media.
Por poner un ejemplo, si se dice que en promedio 1% de la población tiene una cierta enfermedad, seguramente alguien afirmará que si tomamos 100 personas, 1 de ellas la tendrá. Exagerándolo más, si el 50% de la población es mujer, tomando 2 personas, 1 de ellas debe ser mujer.

Un ejemplo real:
19 enero 2018
https://www.lavanguardia.com/politica/20180119/44118665363/ossorioizquierdo-se-equivoco-al-negar-falsedad-sobre-pobreza-ninos-en-madrid.html

Según Ossorio, Izquierdo "quería decir que cuando alguien va por la calle no ve un niño pobre, otro no pobre y otro pobre; es una afirmación falsa de la izquierda, pues esa proporción no se ve en las calles" madrileñas.
Este jueves, en el Pleno monográfico de la Asamblea sobre la protección de la infancia, el portavoz del PSOE-M, Ángel Gabilondo, afirmó que en la Comunidad de Madrid uno de cada tres niños es pobre, a lo que Izquierdo le contestó preguntando: "¿Usted va por la calle y va viendo un niño pobre, uno normal, uno normal?".


https://www2.asambleamadrid.es/DDSS%20LEGISLATURA%20X/X-DS-598.PDF
Voy  a  recordar  la  última,  tan  reciente  que  su  eco  aún sigue  resonando  en  la  sede  parlamentaria,  es  la  pronunciada  en  el  marco  del  debate  monográfico sobre infancia y adolescencia: ¡usted va por la calle  y va  viendo un  niño pobre y  uno normal! Así le preguntó  al  señor  Portavoz  de  mi  Grupo,  al  señor  Gabilondo. 

 

Además del error asociado a muestra pequeña, está el tema del tamaño adecuado / necesario de la muestra, que es algo relevante

https://twitter.com/Picanumeros/status/1685588559649034241

https://threadreaderapp.com/thread/1685588559649034241.html

De acuerdo, pues tal y como prometí ayer, se viene hilo explicando y justificando la respuesta correcta a la consulta de antes de ayer.

¿Vale más coger una gran fracción de la población cuando hacemos una encuesta, o más bien se trata simplemente de coger una muestra grande?

Desprestigiar la información media con cherry picking

A veces se desprestigia la información media poniendo un ejemplo que parece contradecir ese dato.
Por ejemplo, si el 90% de centros privados con concierto contra cuota, segrega... se ponen unos ejemplos que no lo hacen.
Lo puntual no niega lo global.

Se comentan ideas al hablar de segregación.

La media se usa incorrectamente

Pongo ejemplos, igual el de salario es el más comentado, fácil de visualizar y especialmente manipulado, pero yo me voy a educación y empiezo por ratios.

Ratios

La información en general está en Ratios en educación, y luego separado en Ratios en educación: estadísticas y realidad, no voy a repetir todo, cito ideas.

La normativa fija valores de ratios máximos de alumnos por aula, pero se empeñan en dar datos de ratios medios de alumnos para todas las aulas, o de ratios medios de alumnos por profesor, que no son reales.
Madrid reconoció por escrito que, cuando decía que cumplía ratios, eran medias medias, porque incumple ratios máximas: lo resumí así 

Propongo unas analogías para ver que no se puede usar el valor medio, que es ilegal:
-Si el límite de velocidad en una carretera es de 120 km/h, si uno va a 150 km/h es ilegal. No vale decir "es que somos la Comunidad de Madrid, tenemos 1000 coches, voy puntualmente a 150 km/h, en este coche, pero en otros tramos/ con otros coches voy a 80 km/h y la velocidad media de todos mis coches es menor de 120 km/h, no es ilegal"
-Si un vehículo tiene un número de plazas máximas autorizadas a 5, y en uno van 8 personas, es ilegal. No vale decir "es que somos la Comunidad de Madrid, tenemos 1000 coches, vamos puntualmente 8 personas en este coche, pero en otros coches van menos de 5, así que la ocupación media de todos mis coches es inferior a 5, no es ilegal"

En Twitter recuerdo este comentario con una referencia que incorporé al post
IMPORTANTE: Si conoces alguna escuela que haya perdido una de sus clases de tercero de primaria junto a los 13 niños que por estadística le pertenecen, que no busque más, están en mi clase de 26.


¿Cómo es la ratio de alumnos por profesor en el mundo?

Añadido, ya tenía referencia a World Bank que es su fuente... y da estos números de secundaria. A los docentes nos da la risa, pero para los políticos son datos que les dan "su visión estadística de despacho que llaman realidad"

Y otro ejemplo que incorporé de un estudio, cita esta barbaridad
 estimates of pupil-teacher ratios as a proxy for class size, 

Si en los CRA (Centros Rurales Agrupados) hay pocos alumnos por aula, eso baja la ratio media, y puede hacer que la media sea menor que el valor máximo permitido cuando en muchas aulas se supere ese valor.

También hay otras cosas: por ejemplo en religión un grupo se abre sin mínimo de alumnos, y ese profesor computa para hacer la media de alumnos por profesor.
Pendiente comparar valores medios por CCAA y con Europa.

Riqueza

Algunos ejemplos reales en redes
https://twitter.com/lockcda/status/934479657776373760
Entonces, supongamos que usted y yo y su vecino conformamos un país juntos. Y que un país con una riqueza media de 200.000€ se considera rico. Yo tengo 1.000.000€ y usted y su vecino tienen 0€. Los tres hacemos una media de 333.000€. ¿Es un país rico? 2/3 pasan hambre.
https://twitter.com/econolibertad/status/934723672727793664
veo que de estadística no sabes nada En un país con 50 millones de personas, si la riqueza media es de 200.000€ es porque la mayoría tiene una riqueza de 200.000€
https://twitter.com/ProtonC1/status/934817577154568192
No. Mira, con 50 millones de personas, por ejemplo, también habría una riqueza media de 200000€ si el 1% de la población tuviera una riqueza de 20000000€ y el 99% no tuviera nada.

22 enero 2018
"El 1% de los ricos del mundo acumula el 82% de la riqueza global" (y las críticas a estas cifras de Oxfam)
https://www.bbc.com/mundo/noticias-42776299

Salario

También enlaza con "becas" [cheques SOLO para privados] de Madrid 2022
 

Aparte hay algunas fuentes de datos generales con tablas que se van actualizando



Cito este gráfico y este hilo donde creo que el uso de "cagarruta de la derecha del gráfico" es muy ilustrativo de cómo esos valores por encima de 100000 pueden modificar mucho la media
https://twitter.com/indvbio/status/1035431849617702912



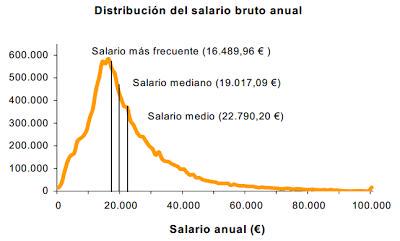
(esos datos los cito en un enlace y creo recordar que son de 2012, no tienen fecha, el hilo sí cita similares con fecha)
Creo que es significativo que el salario más frecuente casi es el mismo, pero el medio sube, y así a ojo creo que se podría decir que es muy similar, pero la "cagarruta de la derecha" más grande aumenta la media.


29 octubre 2012
La mayoría de los trabajadores (62%) gana menos que la media
https://www.ciencia-explicada.com/2012/10/la-mayoria-de-los-trabajadores-62-gana.html

2 noviembre 2012
Media, mediana y moda; versión «a ver si así aprenden a aplicarlas cuando hablen de salarios»

6 agosto 2013
Cuando hables de salarios utiliza la mediana
https://www.gaussianos.com/cuando-hables-de-salarios-utiliza-la-mediana/

6 noviembre 2015
Por qué nos extraña que el salario medio sea de 1881,3 euros
https://verne.elpais.com/verne/2015/11/06/articulo/1446818999_602622.html


20 diciembre 2016
¿Es el salario medio una buena medida del bienestar de un país? El salario mediano
https://www.investigacionyciencia.es/blogs/matematicas/99/posts/es-el-salario-medio-una-buena-medida-del-bienestar-de-un-pas-el-salario-mediano-14810

28 junio 2016
Encuesta de Estructura Salarial 2014
http://www.ine.es/prensa/np977.pdf


8 noviembre 2017
Decil de salarios del empleo principal.
Encuesta de Población Activa (EPA)
Año 2016
https://www.ine.es/prensa/epa_2016_d.pdf

29 mayo 2018

29 enero 2019
Surge un hilo con datos, cita deciles que lo veo como otra manera de dar datos agregados pero en más tramos, más desagregados y da más información que media. Realiza comentarios sobre docentes, contesté con datos memoria RDL14/2012 y no me respondió

https://twitter.com/amjorge15/status/1090019296418377728
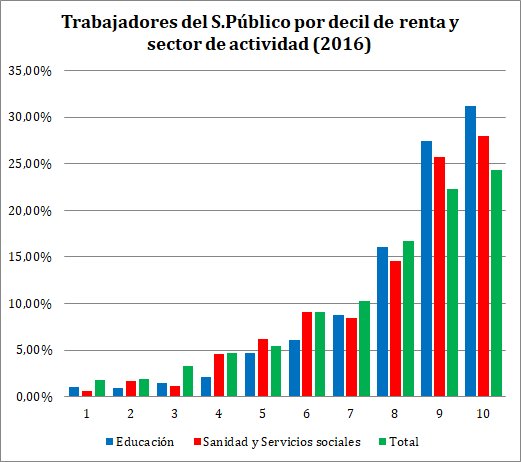
Posición de los empleados públicos en la distribución de la renta. En los deciles 8, 9 y 10 suman 63,4%, % similar a si miramos la distribución salarial salvo que, en el 10, pasan de 20,9% a 24,3%. Es decir, casi 1 de cada 4 de los empleados públicos está en el 10% que más gana.

https://twitter.com/amjorge15/status/1090017707913867267
Para ponerlo con más perspectiva incluyo el total (el gráfico del principio del hilo). Ahora darle una vuelta al conflicto salarial que generó de la marea verde.
https://twitter.com/amjorge15/status/1090295948859846657
El hilo argumenta que se protestó por motivos salariales y no por medios, dando a entender los funcionarios en educación ya están en una posición muy buena
https://twitter.com/amjorge15/status/1090725567656275971
Yo fui a la pública, y de momento no he recibido razones convincentes de que protestaran por la falta de medios en vez de por una cuestión salarial.

Le contesté, sin respuesta
 Datos memoria RDL14/2012 "recortes"; salvo retoques, en vigor. Horario secundaria pasó 18 sesiones lectivas a 20; 9 docentes hacen que antes hacían 10 (18*10=20*9): -10% docentes (casi todo interinos), con más alumnos (+20% ratio) y no cubres bajas 10 días

Desprestigio con el salario medio es habitual


En esta nota de prensa del INE de 24 octubre 2012
http://www.ine.es/prensa/np741.pdf
se dice literalmente esta frase, orientada a un momento en el que justificar recortes a funcionarios
"El salario anual en el sector público fue un 30,8% más alto que el salario medio"

http://www.docentesconeducacion.es/viewtopic.php?f=68&t=1376
Lo comenté aquí

Estaría bien cruzar más datos, pero en principio se me ocurre que, dejando aparte temas de "asesores" y "personal eventual de confianza", para trabajar en el sector público hay que pasar un proceso selectivo y se necesita un nivel de estudios superior, que supone eliminar de la media de los salarios públicos gente con bajo nivel de calificación que sí está en la media del privado cobrando el SMI o poco más
http://www.ine.es/jaxi/tabla.do?path=/t22/p133/a2010/l0/&file=06003.px&type=pcaxis&L=0
Encuesta de estructura salarial. Año 2010
Resultados por Comunidades Autónomas: Distribución salarial
Medias y percentiles por sexo y estudios realizados

Se ve como para el salario medio influye el nivel de estudios: datos nacionales y para ambos sexos.
I. Sin estudios 15.479,21 
II. Educación primaria 17.064,08 
III. Educación secundaria I 17.727,22 
IV. Educación secundaria II 22.691,68
V. Formación profesional de grado medio 20.385,50
VI. Formación profesional de grado superior 23.676,49 
VII. Diplomados universitarios o equivalente 29.104,17 
VIII. Licenciados, ingenieros superiores y doctores 35.864,81 

Si la media nacional de salario son 22790,20, si la media en el privado es menor y en el público es mayor, influirá el nivel de estudios que predomina en cada sector. Venimos de la burbuja del ladrillo, gente trabajando sin estudios por poco dinero ...

15 junio 2019
El sueldo de los funcionarios registrará una subida media de más de 700 euros este año
https://amp.elmundo.es/economia/macroeconomia/2019/06/15/5d03876821efa0b84c8b4600.html


Otro ejemplo de uso de media
21 abril 2019
La evolución de los salarios en Europa
https://elordenmundial.com/mapas/la-evolucion-salarios-en-europa/

Se comenta esto
14 noviembre 2019
https://twitter.com/elOrdenMundial/status/1194819772388696064
Los países europeos en los que menos han crecido los salarios desde la crisis de 2008 (ojo a Grecia).

 🇪🇸España -0,3%
🇬🇧Reino Unido -0,5%
🇮🇹Italia -0,6%
🇬🇷Grecia -3,1%

Y esa media (0,3% puede ni llegar a tener cifras significativas) esconde otra realidad
22 junio 2019
https://twitter.com/BrankoMilan/status/1142531921999777792
Some stunning results for Spain, based on the just-published @lisdata  harmonized survey data. 
Ten years after the crisis, real median income is the same as in 2007, bottom 40% lost in real terms, income of the top 1% went up by 21%. 

26 febrero 2020
Empate de Madrid y el País Vasco en el ranking de salarios más altos: cuánto se cobra en cada CCAA
https://www.idealista.com/news/finanzas/laboral/2020/02/26/780465-empate-de-madrid-y-el-pais-vasco-en-el-ranking-de-salarios-mas-altos-de-espana-cuanto-se
Hay una etiqueta "salario medio españa" en idealista con muchos más
https://www.idealista.com/news/etiquetas/salario-medio-espana

14 julio 2022

¿Sabes cómo de rico eres? Averigua tu posición en la escalera del dinero, por renta y patrimonio
La mayoría de la gente cree que tiene una renta media, pero a menudo se equivoca. Si ganas más de 20.500 euros, estás en la mitad rica, y si superas los 44.000, eres del 10% con más ingresos

http://elpais.com/actualidad/newsletter-kiko-llaneras/2022-07-14/sabes-como-de-rico-eres-averigua-tu-posicion-en-la-escalera-del-dinero-por-renta-y-patrimonio.html

Por cierto, haciendo un inciso, estos datos sirven para poner en contexto las becas públicas en centros privados de Madrid. El Gobierno de la región elevó el límite para que esas ayudas las pudiesen recibir, por ejemplo, parejas con un hijo que ingresen hasta 107.000 euros (entiendo que brutos). Es decir, personas que pueden estar entre el 10% y el 5% con más renta de España.

Cambio climático: cuando la media sí importa 

El caso del calentamiento global es un ejemplo en el que la media sí importa, pero en este caso hay quien presta atención a valores puntuales y no a la media, negando el calentamiento porque puntualmente en una región haga frío. Habrá quien piense que es imposible hacer una media de toda la temperatura globlal, pero sí lo es, y no se le presta la atención que merece.
https://es.wikipedia.org/wiki/Equilibrio_t%C3%A9rmico_de_la_Tierra#Temperatura_de_equilibrio_de_la_atm%C3%B3sfera_terrestre

Pongo un dato reciente
22 marzo 2019
https://www.noaa.gov/news/global-carbon-dioxide-growth-in-2018-reached-4th-highest-on-record


https://twitter.com/RARohde/status/1111592823319609349


https://twitter.com/neilrkaye/status/1225073039538343936
New animation demonstrating the transition from weather to climate. Starting with daily temperature data compared to the long term average, this shows increasingly longer averaging periods up to 30 years to see the warming signal emerging.

#dataviz #climatechange #globalwarming
 
 
Sobre el tema del día, lean este hilo de @dr_xeo. La temperatura no sólo ha aumentado en media (más eventos extremos por calor que por frío), sino también en varianza (eventos de ambos extremos son más probables).
¿Un invierno cada vez más caluroso? Sí, efectivamente. #CambioClimatico Aquí os dejo cuatro ejemplos de diferentes ciudades españolas. Los gráficos representan la distribución de las anomalías de las temperaturas medias diarias en invierno.
ABRO HILO 
1) Los datos en que se basan las distribuciones han sido homogeneizados. Lo que quiere decir que se han corregido posibles saltos y/o cambios no climáticos, por ejemplo, debido a una reubicación o cambios en la instrumentación.
2) La siguiente figura es del IPCC (2013b:134) y explica lo que vemos en los gráficos de la distribución de la temperatura o su anomalía. Los cambios en las frecuencias de los extremos se ven afectados por tres posibilidades estadísticas a) en la media, b) en la varianza o forma,
y c) tanto en la media como en la varianza. En la práctica lo que ya se ha observado es que está cambiando la media y la varianza, o sea, la posibilidad (c). ¿Pero que implica este cambio en la distribución?
3) Cuando aumenta la media (a) nos conduce a más extremos por calor y menos por frío. PERO no significa que no haya eventos extremos por frío, únicamente, su frecuencia será menor. Cuando aumenta la variabilidad (varianza) (b) se puede observar más extremos por calor y frío.
Por último, el caso que corresponde a la realidad, cuando aumenta la media y la variabilidad, sin duda, aumentan los extremos por calor de forma considerable. Por otro lado, los extremos por frío pueden quedar igual o disminuir.
4) Para resumir lo que se observa de forma empírica en los gráficos de distintas ciudades. En invierno, existe claramente un aumento de días con extremos por calor en todas las ciudades y al mismo tiempo una reducción de extremos por frío.
Este cambio es muy visible cuando observamos las curvas (las distribuciones) de las diferentes décadas.
5) Para finalizar este hilo (que es mi primero), os adjunto la distribución de las anomalías en verano a nivel global y los cambios observados por décadas lo que finalmente confirma lo que vemos en las ciudades con datos diarios.  (link: https://giss.nasa.gov/research/briefs/hansen_17/)

 



Gasto por alumno

Es un tema recurrente en educación: cuál es el gasto medio por alumno. Es algo que se puede extrapolar también a la sanidad. Creo que se suele hacer lo más fácil: coger todo el presupuesto público y se divide entre el número total de alumnos, y así se tiene un "gasto medio por alumno". 
El problema es que la desinformación y los intereses citan eso como "gasto por alumno", y llevan a decir:
-El gasto por alumno en la educación privada con concierto es menor: hay que potenciar los conciertos.
-El gasto por alumno si se hiciera educación en casa sería menor: hay que implantar el cheque escolar

Detallar el mantra de la concertada del coste es para otro post (colgará de este post #10MantrasDeLaConcertada), pero creo aparte del valor, que hay un error básico: el coste medio por alumno no es el coste de cada alumno. Un alumno en un CRA, o un ACNEE  tendrá un coste mayor.
  • Los centros concertados no llegan a zonas donde no es rentable la educación, porque allí el coste es mayor. Pero la educación pública, un servicio público, se ofrece sin atender al coste. Y eso lo dice la propia ministra, en un tuit en el que está reconociendo que la concertada puede no ir si no hay negocio
La educación pública es la piedra angular del sistema, del que forman parte la concertada y la privada. Tenemos la obligación de dar una educación de calidad en ciudades y en pueblos pequeños. Ahí puede no llegar la concertada, pero la pública tiene que llegar a todas partes.

  • Los gastos de la gestión educativa se suelen atribuir solamente a la educación pública, pero no a la privada concertada, cuando hay dinero gastado en gestionar el dinero que se está dando a los privados concierto.
Hay un mantra que se repite regularmente, sobre todo cuando los empresarios/empleados/usuarios/ de la privada subvencionada (llamémosla sin eufemismos), ven peligrar sus privilegios. Se refiere al coste del puesto escolar en comparación con la enseñanza pública.
HILO Desde quienes se limitan a decir que el coste en la privada es menor a quienes dicen que es la mitad, el porcentaje varía según la fuente. ...
1 respuesta10 retweets21 Me gusta

  • El cheque escolar (eso es para otro post, pero pongo ideas) lo veo un riesgo al abandonar la responsabilidad del estado en ofrecer un servicio público. No, el estado no puede delegar totalmente la educación en las familias, porque hay familias que pueden usar ese dinero para otras cosas distintas de educar, y porque ese dinero se convertiría en mercancía en el que los padres serían clientes y los centros meras empresas que buscan satisfacción de clientes, desvirtuando el objetivo de la educación. Pero además el cheque tendría posiblemente un importe similar para todos (quizá con modificaciones en función de las circunstancias personales), pero el coste no lo es para cada alumno en función de su situación. Es como ofrecer un seguro de sanidad privado, con ciertas modificaciones en el precio en función de circunstancias personales,  pero que se sabe que no va a cubrir casos graves. En sanidad y educación pública, se presta un servicio público, y da igual el coste: no se deja de escolarizar a un niño con minusvalía ni se deja de tratar un cáncer por el coste en un servicio público. Y además, dar el dinero y la única decisión a los padres supondría dejar en su mano la segregación, que es algo que el estado debe evitar.

A veces se comparan gastos medios entre países
CAPÍTULO 7 LA FINANCIACIÓN DE LA EDUCACIÓN EN ESPAÑA Jorge Calero, (Catedrático de Economía Aplicada, Universidad de Barcelona) y Xavier Bonal (Profesor de Sociología, Universidad Autónoma de Barcelona)
http://sid.usal.es/idocs/F8/FDO6750/08cap7.pdf

Dentro de la U.E., únicamente Grecia e Irlanda  presentan  niveles  de  gasto  público  educativo  más  bajos  que  España.  El  valor del indicador se sitúa en España un punto porcentual por debajo de la media europea; 
...
El gasto en institucioneseducativas por alumno en 2001, en dólares USA corregidos mediante ppc(5), es en España, en primaria, 3.941 (la media de la OCDE es 4.698); en secundaria, 5.185 (media OCDE de 6.303) y, en superior, 6.666 (media OCDE de 9.413).

Segregación alumnos

Cuando se habla de segregación de alumnos (de nuevo enlaza con mantras de concertadas y se trata en posts dentro de la serie #10MantrasDeLaConcertada), suelen decir que la concertada no segrega.
La segregación es de varios tipos, por ejemplo nivel socioeconómico, país de origen y alumnos ACNEE

  • Para el nivel socioeconómico es un hecho, pero cuando se pregunta se suelen citar casos puntuales de centros privados concertados en zonas desfavorecidas, sin nombres y sin citar las medias.
1- La concertada no es el único problema, pero sí es el principal factor de segregación. Las escuelas concertadas expulsan a las familias sin recursos, hasta el punto de que la concertada asume menos de la mitad de los alumnos pobres que le tocarían.

Lo cito en el post Correlación en educación

30 septiembre 2019
Escuela de ricos, escuela de pobres? Cómo la concertada y la pública segregan por clase social
El análisis de todos los centros de España y la renta de sus vecindarios explica cómo la desigualdad afecta al sistema educativo
https://elpais.com/sociedad/2019/09/30/actualidad/1569832939_154094.html


Gran trabajo cruzando datos de renta con tipos de centros.
Esta gráfica es contundente



  • Para país de origen, los datos son abrumadores
¿Excluyente la concertada? La normativa de admisión de alumnos es exactamente la misma en pública y concertada. Los centros apenas intervienen en los procesos de admisión controlados por programas informáticos de las Adminitraciones públicas
Le ruego cuelgue aquí esos porcentajes de los que habla y los debatimos.

Por si resultan de interés para el debate. datos avance 2017/2018, enseñanzas no universitarias alumno extranjero por titularidad del centro, y enseñanza. Saludos


Los datos globales aquí
https://twitter.com/FiQuiPedia/status/1209178117358706692
#10MantrasDeLaConcertada
Datos con fuente.
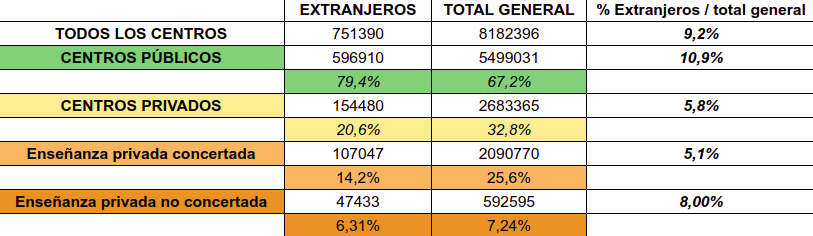
La pública tiene el 80% alumnado extranjero, 67% alumnado: el 11% de su alumnado.
Privados con concierto tienen 14% alumnado extranjero, y 26% alumnado: el 5% de su alumnado.
Saca la conclusión
https://docs.google.com/spreadsheets/d/1tD8Xt2fMgi6p4s-JCPQtx7TPqzjsyUP-58JhrtQetFo/edit#gid=0


Pero todavía hay más sobre esta media, y enlaza con el cherry picking: cada vez que se intenta poner como argumento de que los privados con concierto la existencia de un centro con alto número de inmigrantes, se está mostrando que para que la medida tenga ese valor, existiendo ese centro, la segregación es mayor en el resto.

https://www.magisnet.com/2020/07/demagogia-publica-y-concertada/
Lo que ha hecho el Gobierno sería tanto como privar de ayudas a todas las familias de aquellas comunidades autónomas que superen la renta media del país.




https://twitter.com/FiQuiPedia/status/1280133965274365955
Lo puntual no niega lo global.
Aquí aporto datos, con fuente, que muestran que globalmente los privados con concierto segregan. ¿Puedes aportar fuente de ese 98%? Cada cherry picking %alto confirma que en otros privados con concierto es menor a 5,1%.



26 septiembre 2018
El colegio con un 2% de españoles que desafía la segregación escolar y despunta con sus resultados académicos
https://www.eldiario.es/nidos/colegio-espanoles-desafia-segregacion-escolar_1_1922378.html

En el San Antonio, religioso de inspiración franciscana y concertado pero de cuota 0, ya que la congregación cubre con sus propios ingresos la parte que en otros centros de este tipo pagan las familias, casi todos los alumnos tienen un nivel económico bajo o están en riesgo de exclusión social.

San Antonio Multicultural
https://redined.mecd.gob.es/xmlui/bitstream/handle/11162/92071/00820113014534.pdf?sequence=1





  • Para ACNEE, creo que se suelen hacer medias incluyendo los alumnos de los Centros de Educación Especial, con lo que en función del número de centros de educación especial que haya, la media se aproxima al valor de los centros públicos con ACNEE en aulas ordinarias. También se puede ver post sobre orientación concertada, y ver como en Aragón quisieron arreglar los datos sobrediagnosticando como ACNEE a superdotados

Algunas referencias

2010
UNA VALORACION DEL GRADO DE SEGREGACIÓN SOCIOECONÓMICA EXISTENTE EN EL SISTEMA EDUCATIVO ESPAÑOL. UN ANALISIS POR COMUNIDADES AUTONÓMAS A PARTIR DE PISA 2006
MANCEBÓN TORRUBIA, María Jesús
PÉREZ XIMÉNEZ-DE-EMBÚN, Domingo. 
Los alumnos más selectos se concentran mayoritariamente en los centros privados, si bien su repartoentre las diferentes escuelas es bastante heterogéneo, especialmente en la enseñanza privada no concertada. En el sector público, los estudiantes presentan un perfil socioeconómico mucho más homogéneo entre los diversos centros, agrupándose en todos ellos los alumnos pertenecientes a los hogares de menos recursos económicos y culturales y los inmigrantes.

Conciertos educativos y selección académica y social del alumnado

Jesús Mancebón Torrubia Mª (mjmance@unizar.es) and Domingo Pérez-Ximénez de Embún (dpxe@unizar.es)
Additional contact information
Authors registered in the RePEc Author Service: María Jesús Mancebón-Torrubia (mjmance@unizar.es) and Domingo Pérez Ximénez-de-Embún (dpxe@unizar.es)
Hacienda Pública Española, 2007, vol. 180, issue 1, 77-108
El análisis de las características de los alumnos que eligen un centro concertado realizado en la última sección del artículo mediante la especificación de un modelo probit permite además apreciar una relación significativa entre el nivel académico y socioeconómico y la elección de centro privado concertado, indicando que la segregación intersectorial encontrada en el trabajo puede ser atribuida en parte al patrón de elección de los usuarios del sistema educativo.


Magnitud de la segregación escolar por nivel socioeconómico en España y sus Comunidades Autónomas y comparación con los países de la Unión Europea
La segregación escolar en las Comunidades ofrece resultados extremos, algunas se encuentran entre las más bajas de Europa (Illes Balears, Galicia y Aragón) y otras como la Comunidad de Madrid con una segregación muy alta, solo superada por Hungría dentro de la Unión Europea. Con todo ello se observa la incidencia de las políticas educativas regionales respecto a los criterios de admi-sión de centros en la segregación escolar, mostrando que políticas como el fomento de la educación privada, de la competencia de centros mediante la publicación de rankings o la creación de un distrito único pueden configurar sistemas educativos inequitativos que atentan a la igualdad de oportunidades.

19 octubre 2019
https://twitter.com/lcentenoc/status/1185597988388954112
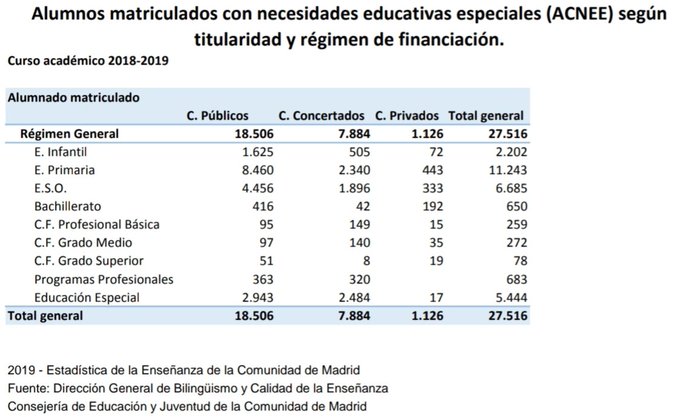
El 50 % de los alumnos con necesidades educativas especiales se escolarizan en Centros concertados. Y la concertada representa sólo el 20 % del sistema educativo. Saca la conclusión.

Para validar la hipótesis sobre los centros de EE, que supone que en los centros privados con concierto casi no hay ACNEE, hay que tener datos de alumnos en EE desglosado por titularidad

Datos y Cifras de la Educación2018-2019
http://www.madrid.org/bvirtual/BVCM016418.pdfTabla 1. Alumnos matriculados en Enseñanzas de Régimen General por enseñanzas, titularidad y régimen de financiación del centro
2017-2018
Educación especial
C. públicos 2.892
C. concertados 2.452

 http://www.educacionyfp.gob.es/dam/jcr:b998eea2-76c0-4466-946e-965698e9498d/datosycifras1920esp.pdf
Alumnado en Enseñanzas no universitarias por sexo y titularidad del centro. Curso 2018-2019
E. Especial 37.302
% Centros públicos 60,4
% Enseñanza concertada (2) 39,3
(2=  Se ha estimado la distribución de la enseñanza privada en concertada y no concertada a partir de los datos delcurso 2017-2018.)

https://twitter.com/FiQuiPedia/status/1185856312619470848

20 octubre 2019
Planteo petición a Madrid
---
Solicito datos de número de alumnado con necesidades específicas de educación (ACNEE) con el mismo desglose por titularidad y régimen de financiación del centro con el que se facilitan datos y Cifras de la Educación 2018-2019
http://www.madrid.org/bvirtual/BVCM016418.pdf
donde se indica, sobre alumnos matriculados en Enseñanzas de Régimen General, desglosado por titularidad y régimen de financiación del centro
-alumnado por enseñanza (tabla 1)
-alumnado extranjero (tabla 3)
-alumnado por nacionalidad (tabla 4)
Los datos de número de ACNEE solicitados son manejados por la administración, ya que tienen un dictamen oficial y para atender las necesidades de cada caso requieren recursos adicionales por parte de la administración.
---
Referencia 49/589789.9/19

30 octubre 2019
Recibo resolución
https://drive.google.com/open?id=1PVacE9I_E8MAaCemnGV-3Vb3v0FYUhiS
y datos
https://drive.google.com/open?id=1PYY4Wc-0y2jarBRPNaLFEJE0_h8jkt55
los datos citan "2019 - Estadística de la Enseñanza de la Comunidad de Madrid" y tienen "el formato" de https://estadisticas.educa.madrid.org/
pero ahí no están disponibles.

Lo comento aquí
https://twitter.com/FiQuiPedia/status/1189483887824691200
Como @lcentenoc  no aporta datos, los aporto yo, con su fuente.
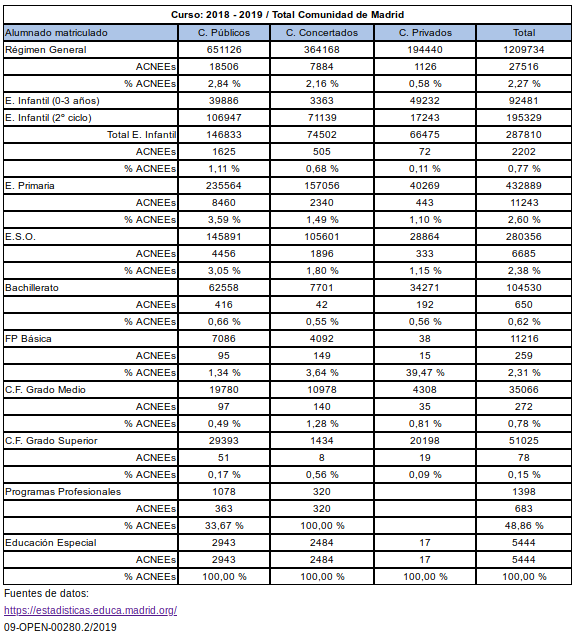
Madrid, ACNEEs pública vs privada con concierto:
•Primaria: 3,6 veces más
•ESO: 2,4 veces más
Recibidos así; se puede hacer % sobre alumnado.


Planteo los datos para verlo en %
https://estadisticas.educa.madrid.org/Report/ReportTemplate?ReportName=01_Alumnos_MatricTitularidadEnsenanzas&ReportDescription=Alumnos%20matriculados%20en%20Ense%C3%B1anzas%20de%20R%C3%A9gimen%20General%20por%20ense%C3%B1anzas%2C%20titularidad%20y%20r%C3%A9gimen%20de%20financiaci%C3%B3n%20del%20centro&Width=100&Height=650

Lo comparto aquí
https://drive.google.com/open?id=1P-N1wM60up_BHbgFGN4dmOHTaixi5sJo

Más datos en ministerio
https://www.educacionyfp.gob.es/servicios-al-ciudadano/estadisticas/no-universitaria/alumnado/necesidades-apoyo/2017-18.html


Calificaciones medias

Dar la calificación media es algo que no tiene sentido sin dejar muy clara la muestra y el contexto, enlaza con LOMCE: finalidad evaluación para clasificación centros en la que la clasificación se hace con medias.


14 junio 2019
Las aulas que usan Google suben las notas medias
Expertos analizan en la UJI el uso de herramientas digitales como medio didáctico
https://amp.elmundo.es/comunidad-valenciana/castellon/2019/06/14/5d037223fdddffcc018b45ba.html

Zubiria explica uno de los trabajos de investigación que el grupo desarrolla cada curso en este ámbito. «Testamos en las clases las herramientas de Google para la educación, lo que se conoce como entorno Gsuite, y las evaluamos para luego comparar a estos alumnos que las usan con otros estudiantes de una clase espejo que no las utilizan».
Los resultados de este testeo hablan de que los alumnos que utilizan estas herramientas de Google en clase se sienten más motivados, asisten más al aula y prestan más atención además de contar con una nota media más alta que su clase espejo.

https://twitter.com/AntVargRey/status/1139937194267860993
– Llaman grupo espejo al grupo de control.
– Los alumnos saben a que grupo pertenece.
– Los investigadores saben a que grupo pertenece cada alumno.
– Los que han analizado los datos son los propios investigadores.
¿Y me tengo que fiar de sus conclusiones? ¡¡ANDA YA!!

Gasto por persona e impuestos

Está relacionado con el gasto medio por alumno e idea de cheque escolar: no se puede pretender que todo el mundo pague el mismo coste y sea el coste medio, sino que algunos tienen que pagar más y otros menos, progresivo según lo que tienen, permitiendo que el gasto real por persona pueda cubrir gastos que van mucho más allá de la media:
En general los impuestos están "demonizados", pero es una medida que hace que el gasto de un servicio público como sanidad y educación sea viable para personas que lo tienen mucho mayor, compensando con las que lo tienen menor.
En sistemas como EEUU sin sistema sanitario público basado en impuestos no es extraño entrar en bancarrota por una atención sanitaria puntual.
Hace unas semanas, Sanidad publicó algo que a mí me parece clave sobre esto: el coste medio de los ingresos más frecuentes. Creo recordar, x ej, que un bebé prematuro eran 90.000 euros. ¿Cuántos años hay que pagar impuestos para llegar a esa cifra?

En España, el coste medio del ingreso hospitalario por paciente es de 5.092 euros. Pero las diferencias entre unas operaciones según sus características pueden disparar o rebajar el coste. Lo primero que aumenta los recursos de una intervención, explican los expertos, es el paso por la UCI. Cada día en cuidados intensivos cuesta una media de 1.000 euros por persona, lejos de los 300 o 400 que supone estar en planta, debido al gasto de tener a un enfermero por cada dos pacientes y al equipamiento técnico necesario para las emergencias. Incluso los colchones son más caros que los de planta. Por eso, la traqueostomía con ventilación mecánica es la intervención quirúrgica más cara de toda la lista, con 96.000 euros de media, aunque es muy poco frecuente.

A la traqueostomía le siguen en coste los partos de neonatos, por la cantidad de días y atención que necesitan en la planta de neonatología —otra de las más caras—. Un nacido antes de tiempo puede llegar en su caso más complejo a los 90.000 euros. Después se encuentran los trasplantes. Uno de pulmón cuesta casi 69.000 euros; uno de médula, 56.000, y el de riñón y páncreas ronda los 61.000. En el caso de este tipo de operaciones, lo que eleva el coste es la cantidad de días en el hospital que requieren y la logística que rodea la intervención: la necesidad de un equipo completo las 24 horas, que los órganos vayan de un punto a otro en poco tiempo… La técnica y el equipamiento, sin embargo, ya no son tan caros por los avances médicos. De hecho, en España los trasplantes cuestan entre ocho y 10 veces menos que en Estados Unidos, aunque también influye la retribución de los médicos, muy por debajo en el caso español.
Pero aunque estén entre los procesos más caros, los trasplantes abaratan los costes a la sanidad pública en el corto plazo. “En un trasplante renal, por ejemplo, es más barato realizar el trasplante a que el paciente continúe con una diálisis”, explica Beatriz Domínguez-Gil, directora de la Organización Nacional de Trasplantes. “Cada año el sistema de donación y trasplante ahorra al sistema nacional de salud dos veces el coste en diálisis, además del aumento en la calidad de vida”. Se calcula que la diálisis tiene un coste medio de unos 50.000 euros anuales, mientras que el trasplante renal se sitúa en 22.369 euros.


Se cita https://www.rechosp.org/rech/faces/es/jsf/index.jsp

Clase media

Es un concepto que combina riqueza, salario e impuestos
Según la RAE

1. f. Conjunto social integrado por personas cuyos ingresos les permiten una vida desahogada en un mayor o menor grado.

Es un término muy usado a la hora de hablar de impuestos, porque se suele vender como incorrecto subirlos "a la clase media", pero cada político (que toman las decisiones sobre impuestos) quiere entender una cosa sobre dónde está la clase media, aparte de que cada ciudadano quiere verse o no como clase media.

 A algunos políticos les interesa vender como "clase media" rentas altas, ver post Sueldo docentes públicos y subida impuestos a rentas altas
En cierto modo a ciertas "rentas altas" les interesa decir que son "rentas medias" para poder beneficiarse de que las rentas medias tengan impuestos más bajos que las rentas altas.
También hay cierto sesgo en los ciudadanos, que no quieren verse como rentas bajas por el estigma que supone y se autoclasifican en clase media, cuando a menudo no lo son. Hay quien piensa que no es un obrero porque no trabaja con un mono, pero la mayor parte de los asalariados por cuenta ajena son obreros y deben luchar por sus derechos y su renta.


Octubre 2018
https://ctxt.es/es/20181024/Firmas/22540/el-mentidero-clase-media-no-existe-ciudadanos-albert-rivera-cervantesFAQs.htm


Se cita este hilo
https://twitter.com/Mentidero_ctxt/status/1056101225769394178
La clase media no existe. No solo no existe, sino que las derechas son expertas en hacernos pensar que pertenecemos a ella, decir que defienden esos intereses y, por tanto, matar la conciencia obrera. @CervantesFAQs desmonta aquí a la inexistente clase media trabajadora


Tiempos medios

Enlaza con el ejemplo del tiempo de espera media el autobús.
A veces se citan como plazos: listas de espera en sanidad, plazo para conseguir  un destino definitivo como docente en cierta especialidad, plazo medio de pago o de cobro, plazos de resolución de un juicio, ...

Al igual que en las ratios, la normativa suele fijar un valor límite, pero la administración lo incumple y se limita a hablar de valores medios.

2 junio 2019
Administraciones morosas
Asturias, con 19,1 días, es la tercera comunidad que menos tarda en pagar a sus proveedores
https://www.elcomercio.es/economia/administraciones-morosas-20190602014217-ntvo_amp.html
Los 30 días que estipula la Ley de Contratos del Sector Público es un plazo que vulneran sistemáticamente algunas comunidades autónomas. No parece justo que la sanción impuesta al contribuyente que se retrasa en el abono de un tributo sea inmensamente mayor que la que penaliza a la Administración cuando demora una liquidación.




Se cita
Ley 9/2017, de 8 de noviembre, de Contratos del Sector Público, por la que se transponen al ordenamiento jurídico español las Directivas del Parlamento Europeo y del Consejo 2014/23/UE y 2014/24/UE, de 26 de febrero de 2014.
https://www.boe.es/buscar/act.php?id=BOE-A-2017-12902






Por ejemplo artículo 198

4. La Administración tendrá la obligación de abonar el precio dentro de los treinta días siguientes a la fecha de aprobación...




Algunas ideas pendientes

Las anoto para futuras revisiones del post, son ideas de tomar o dar información a medias.
  • Datos de empleo sin tener en cuenta media jornada / parcial. A menudo se dice que se crean empleos, pero de nuevo lo veo manipulación: si se destruyen 10 empleos a jornada completa y se crean 20 a media jornada para realizar el mismo trabajo, la estadística dirá que se han creado 10 empleos más.
    En 2018 un 36% de los empleos fueron a jornada parcial
    https://www.eldiario.es/economia/buenos-empleo-siguen-temporalidad-precariedad_0_853214881.html
  • Titulados en ESO: es algo que enlaza con post ESO parece pero ESO no es. Creo que los datos de titulados en ESO tras la LOMCE y FPB deberían desglosarse para mostrar la realidad.
  • Esperanza de vida: creo que más que debido a que aumente mucho la edad máxima, la esperanza de vida sube porque es un valor medio y la mortalidad infantil ha bajado mucho y eso influye mucho en esa media. Me gustaría validar o refutar la idea con datos. Enlaza con tema de pensiones: se cita que no son sostenibles porque sube la esperanza de vida.
  • Calificaciones: la media puede ser un 5 si la mitad de la clase tiene un 10 y la otra mitad un 0. En realidad suele tender a una gaussiana, pero más bien es una gaussiana de aprobados más otra de suspensos.
  • Terraplanismo: creo que se puede ver como un caso de tomar "valores medios de curvatura" con un muestra pequeña de la superficie donde parece plana, ignorando la visión global.
  • Jornada docente "media": tanto en jornada lectiva, como anualmente, comparando medias entre CCAA, con unión europea. 
  • Media en valores de contaminación
    https://twitter.com/FiQuiPedia/status/1146402729012711425
  • Valores medios y humor
    https://www.elmundotoday.com/2017/10/el-valor-de-x-se-establece-en-5-de-una-vez-por-todas/
    Para remediar esta situación, el instituto ha recogido los resultados de x en miles de cálculos realizados en los últimos 100 años, estableciendo como media el valor 5.149.291. “Como es una cifra muy compleja, la redondeamos a 5”, dice Rascop.

Otras lecturas

Lying with Statistics - Examples of abuse of statistical, mathematical and scientific principles


Statisticians want to abandon science’s standard measure of ‘significance’
Here’s why “statistically significant” shouldn’t be a stamp of scientific approval
https://www.sciencenews.org/article/statisticians-standard-measure-significance-p-values
In science, the success of an experiment is often determined by a measure called “statistical significance.” A result is considered to be “significant” if the difference observed in the experiment between groups (of people, plants, animals and so on) would be very unlikely if no difference actually exists. The common cutoff for “very unlikely” is that you’d see a difference as big or bigger only 5 percent of the time if it wasn’t really there — a cutoff that might seem, at first blush, very strict.

...

Where did the idea for statistical significance come from?

Many scientists now interpret P equal to 0.05 as a cutoff between an experiment that “worked” and one that didn’t. That cutoff can be attributed to one man: famed 20th century statistician Ronald Fisher. In a 1925 monograph, Fisher offered a simple test that research scientists could use to produce a P value. And he offered the cutoff of P equals 0.05, saying “it is convenient to take this point as a limit in judging whether a deviation [a difference between groups] is to be considered significant or not.”
That “convenient” suggestion has reverberated far beyond what Fisher probably intended. In 2015, more than 96 percent of papers in the PubMed database of biomedical and life science papers boasted results with P less than or equal to 0.05.


Handy statistical lexicon
https://statmodeling.stat.columbia.edu/2009/05/24/handy_statistic/
(citado en post Leyes epónimas)

Encontrado vía este tuit que cita correlación y muestras
https://twitter.com/SolEnFlandes/status/1089595213222502405
Handy statistical lexicon. 
Example: "Correlation does not even imply correlation." 😜 
"That is, correlation in the data you happen to have (even if it happens to be 'statistically significant') does not necessarily imply correlation in the population of interest." #Statistics

https://twitter.com/Carnage4Life/status/1246579721585868800
You can teach an entire semester of how to lie with statistics with the y-axis of this chart.



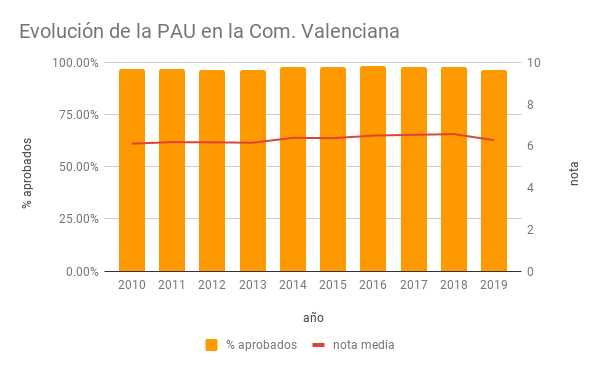
Comentarios

Publicar un comentario

Entradas populares de este blog

Oposiciones: transparencia enunciados

Imagen
Revisado 10 marzo 2021 Resumen Si lo que buscas son enunciados de oposiciones docentes para descargar, puedes mirar aquí https://drive.google.com/open?id=1sfexgtJ2qpGpO4b63zjf2eIC_1ocg2mr Ahí comparto los que, tras reclamar, me han enviado (y algunos que han publicado tras reclamar, aunque los publicados a veces no los descargo y están en la web de la consejería correspondiente), junto con documentación asociada al proceso de conseguirlos. Algunos de Física y Química los tengo en http://www.fiquipedia.es/home/recursos/recursos-para-oposiciones#TOC-Problemas-del-pr-ctico-por-comunidades .  En 2021 realizo una recopilación de todos los problemas resueltos en un único pdf http://cloud.educa.madrid.org/index.php/s/QApVofTSrejPu2W Si te interesa saber cómo reclamar más usando transparencia, puedes seguir leyendo. Por favor: no me pidas que te envíe individualmente algo que ya comparto. Son ficheros voluminosos y comparto tal cual los he recibido: si te da error, revisa (a veces da erro
Leer más

Configurar cliente para leer correo EducaMadrid

Imagen
Revisado 17 marzo 2021 Resumen Con la suspensión de las clases presenciales el uso de la plataforma EducaMadrid crece mucho y al inicio se colapsa (en abril se dota de más recursos y mejora). Además de la labor que se está haciendo a nivel técnico, y de reclamar más recursos si se quiere que de verdad Madrid tenga un servicio para todos con software libre, todo lo que se pueda hacer para facilitar su uso y reducir la carga innecesaria creo que puede útil. Comento aquí una idea asociada al correo corporativo: todos los docentes tienen una cuenta @educa.madrid.org y todos los alumnos también la tienen o la pueden tener (en algunos IES se les asigna automáticamente como los IES tecnológicos, y en otros puede variar, aunque cada vez es más frecuente que la tengan todos los alumnos) En abril 2020 veo que usar gmail como cliente supone que gmail almacena usuario y contraseña (aparte de correos) fuera de la UE, lo que es incorrecto, y dejo de hacerlo.  En mayo 2020 se prohíbe oficialmen
Leer más